Floating point numbers — Sand or dirt
Rudy Velthuis
Rudy Velthuis
[SHOWTOGROUPS=4,20]
Experienced floating point users will know that this can be expected, but many people using floating point numbers use them rather naïvely, and they don’t really know how they “work”, what their limitations are, and why certain errors are likely to happen or how they can be avoided. Anyone using them should know a little bit about them. This article explains them from my point of view, i.e. facts I found out the hard way. It may be slightly inaccurate, and probably incomplete, but it should help in understanding floating point, its uses and its limitations. It does not use any complicated formulas or higher scientific explanations.
Floating point types in Delphi
Floating point is the internal format in which “real” numbers, like 0.0745 or 3.141592 are stored. Unlike fixed point representations, which are simply integers scaled by a fixed amount — an example is Delphi’s Currency type — they can represent very large and very tiny values in the same format.
While Delphi knows several types with differing precision, the principles behind them are (almost) the same.
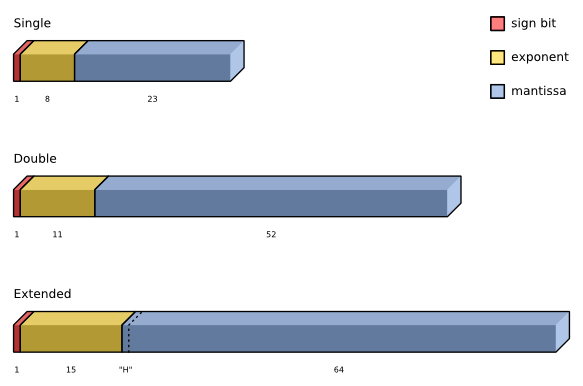
The types Single, Double and Extended are supported by the hardware (by the FPU — floating point unit) of most current computers and follow the IEEE 754 binary format specs.
The type Real, which is a relict of old Pascal, now maps to Double by default, but, if you set {$REALCOMPATIBILITY ON}, it maps to Real48 type, which is not an IEEE type and used to be managed by the runtime system, that is, in software, and not by hardware.
There is also a Comp type, but this is in fact not a floating point type, it is an Int64 which is supported and calculated by the FPU.
The Real48 type is pretty obsolete, and should only be used if it is absolutely necessary, e.g. to read in files that contain them. Even then it is probably best to convert them to, say, Double, store those in a new file and discard the old file.
While Real types used to be managed in software, for computers that did not have an FPU (which was not uncommon in the earlier days of Turbo Pascal), this is not the case for current systems, which have an FPU.
The runtime converts Real48 to Extended, uses that to do the required calculations and then converts the result back to Real48. This constant conversion makes the type pretty slow, so you should really, really avoid it.
Note that the above does not apply to Real, if it is mapped to Double, which is the default setting. It only applies to the 6-byte Real48 type.
Real numbers
There are several ways in which real numbers can be represented. In written form, the usual way is to represent them as a string of digits, and the decimal point is represented by a ‘.’, e.g. 12345.678 or 0.0000345. Another way is to use scientific notation, which means that the number is scaled by powers of 10 to, usually, a number between 1 and 10, e.g. 12345.678 is represented as 1.2345678 × 104 or, in short form (the one Delphi uses), as 1.2345678e4.
Internal representation
The way such "real" numbers are represented internally differs a bit from the written notation. The fixed point type Currency is simply stored as a 64 bit integer, but by convention its decimal point is said to be 4 places from the right, i.e. you must divide the integer by 10000 to get the value it is supposed to represent. So the number 3.76 is internally stored as 37600. The type was meant to be used for currencies, but that the type only has 4 decimals means that calculations other than addition or subtraction can cause inaccuracies that are often not tolerable.
The floating point types used in Delphi have an internal representation that is much more like scientific notation. There is an unsigned integer (its size in bit depends on the type) that represents the digits of the number, the mantissa, and a number that represents the scale, in our case in powers of 2 instead of 10, the exponent. There is also a separate sign bit, which is 1 if the number is negative. So in floating point, a number can be represented as:
value = (−1)sign × (mantissa / 2len−1) × 2exp
where sign is the value of the sign bit, mantissa is the mantissa as unsigned integer (more about this later), len is the length of the mantissa in bits, and exp is the exponent.
Mantissa
The mantissa (The IEEE calls it “significand”, but this is a neologism which means something like “which is to be signified”, and in my opinion, that doesn’t make any sense) can be viewed in two ways. Let’s disregard the exponent for the moment, and assume that its value is thus that the number 1.75 is represented by the mantissa. Many texts will tell you that the implicit binary point is viewed to be directly right of the topmost bit of the mantissa, i.e. that the topmost bit represents 20, the one below that 2−1, etc., so a mantissa of binary 1.1100 0000 0000 000 represents 1.0 + 0.5 + 0.25 = 1.75.
Other, but not so many texts, simply treat the mantissa as an unsigned integer, scaled by 2len−1, where len is the size of the mantissa in bits. In other words, a mantissa of 1110 0000 0000 0000 binary or 57344 in decimal is scaled by 215 = 32768 to give you 57344 / 32768 = 1.75 too. As you see, it doesn’t really matter how you approach it, the result is the same.
Exponent
The exponent is the power of 2 by which the mantissa must be multiplied to get the number that is represented. Internally, the exponent is often “biased”, i.e. it is not stored as a signed number, it is stored as unsigned, and the extremes often have special meanings for the number. This means that, to get the actual value of the exponent, you must subtract a constant value from the stored exponent. For instance, the bias for Single is 127. The value of the bias depends on the size of the exponent in bits and is chosen thus, that the smallest normalized value (more about that later) can be reciprocated without overflow.
There are also floating point systems that have a decimal based exponent, i.e. where the value of the exponent represents powers of 10. Examples are the Decimal type used in certain databases and the — slightly incompatible — Decimal type used in Microsoft .NET. The latter uses a 96 bit integer to represent the digits, 1 bit to represent the sign (+ or −) and 5 bits to represent a negative power of 10 (0 up to 28).
The number 123.45678 is represented as 12345678 × 10−5. I have written an almost exact native copy of the Decimal type to be used by Delphi. It is a little faster than the original .NET type, but not nearly as fast as the hardware supported types.
This article mainly discusses the floating point types used in Delphi, to know Single, Double and Extended, which are all floating binary point types. Floating decimal point types like Decimal are not supported by the hardware or by Delphi. So if, in this article, I speak of "floating point" I mean the floating binary point types.
Sign bit
The sign bit is quite simple. If the bit is 1, the number is negative, otherwise it is positive. It is totally independent of the mantissa, so there is no need for a Для просмотра ссылки Войдиили Зарегистрируйся representation for negative numbers. Zero has a special representation, and you can actually even have −0 and +0 values.
Normalization and the hidden bit
I’ll try to explain normalization and denormals with normal scientific notation first.
Take the values 6.123 × 10−22, 612.3 × 10−24 and 61.23 × 10−23 (or 6.123e-22, 612.3e-24 and 61.23e-23 respectively). They all denote the same value, but they have a different representation. To avoid this, let’s make a rule that there can only be one (non-zero) digit to the left of the decimal point. This is called normalization.
Something similar is done with binary floating point too. Since this is binary, there is only one digit left: 1. So there can only be one (non-zero) digit (always 1) to the left of the binary point. Since this is always the same digit, it does not have to be stored, it can be implied. This is the so-called hidden bit. The types Single and Double do not store that bit, but assume it is there in calculations.
How is this done in binary? Let’s take the number 0.375. This can be calculated as 2−2 + 2−3 (0.25 + 0.125), or, in a mantissa, 0.011…bin (disregarding the trailing zeroes), i.e. 0.375 × 20. But this is not how floating point numbers are usually stored. The exponent is adjusted thus, that the mantissa always has its top bit set, except for some special numbers, like 0 or the so called “tiny” (denormalized) values. So the mantissa becomes 1.100…bin and the exponent is decremented by 2.
This number still represents the value 0.375, but now as 1.5 × 2−2. This is how normalization works for binary floating point. It ensures that 1.0 <= mantissa (including hidden bit) < 2.0. Because of the hidden bit, to calculate the value of such a floating point type, you must mentally put the implicit “1.bin” in front of the stored bits of the mantissa.
Note that in e.g. the language C, the value FLT_MIN stands for the smallest (positive) normalized value. You can have values smaller than that, but they will be denormal values, i.e. with a lower precision than 24 bits.
There is some confusion about how to denote the size (or length, as it is often called) of the mantissa of a type with a hidden bit. Some will use the actually stored length in bits, while others also count the hidden bit. For instance, a Single has 23 bits of storage reserved for the mantissa. Some will call the length of the mantissa 23, while others will count the hidden bit too and call it a length of 24.
[/SHOWTOGROUPS]
Real numbers are a very important part of real life and of programming too. Almost every computer language has data types for them. Most of the time, they come in the form of (binary) floating point datatypes, since those are directly supported by most processors. But these computerized representations of real numbers are often badly understood. This can lead to bad assumptions, mistakes and errors as well as reports like: "The compiler has a bug, this always shows ‘not equal’"Floating point numbers are like piles of sand; every time you move them around, you lose a little sand and pick up a little dirt. — Brian Kernighan and P.J. Plauger
Код:
var
F: Single;
begin
F := 0.1;
if F = 0.1 then
ShowMessage('equal')
else
ShowMessage('not equal');
end;Experienced floating point users will know that this can be expected, but many people using floating point numbers use them rather naïvely, and they don’t really know how they “work”, what their limitations are, and why certain errors are likely to happen or how they can be avoided. Anyone using them should know a little bit about them. This article explains them from my point of view, i.e. facts I found out the hard way. It may be slightly inaccurate, and probably incomplete, but it should help in understanding floating point, its uses and its limitations. It does not use any complicated formulas or higher scientific explanations.
Floating point types in Delphi
Floating point is the internal format in which “real” numbers, like 0.0745 or 3.141592 are stored. Unlike fixed point representations, which are simply integers scaled by a fixed amount — an example is Delphi’s Currency type — they can represent very large and very tiny values in the same format.
While Delphi knows several types with differing precision, the principles behind them are (almost) the same.
The types Single, Double and Extended are supported by the hardware (by the FPU — floating point unit) of most current computers and follow the IEEE 754 binary format specs.
The type Real, which is a relict of old Pascal, now maps to Double by default, but, if you set {$REALCOMPATIBILITY ON}, it maps to Real48 type, which is not an IEEE type and used to be managed by the runtime system, that is, in software, and not by hardware.
There is also a Comp type, but this is in fact not a floating point type, it is an Int64 which is supported and calculated by the FPU.
The Real48 type is pretty obsolete, and should only be used if it is absolutely necessary, e.g. to read in files that contain them. Even then it is probably best to convert them to, say, Double, store those in a new file and discard the old file.
While Real types used to be managed in software, for computers that did not have an FPU (which was not uncommon in the earlier days of Turbo Pascal), this is not the case for current systems, which have an FPU.
The runtime converts Real48 to Extended, uses that to do the required calculations and then converts the result back to Real48. This constant conversion makes the type pretty slow, so you should really, really avoid it.
Note that the above does not apply to Real, if it is mapped to Double, which is the default setting. It only applies to the 6-byte Real48 type.
Real numbers
The real-number system is a continuum containing real values from minus infinity (−∞) to plus infinity(+∞). But in a computer, where they are only represented in a very limited amount of bytes (Extended, the largest floating point type in Delphi, has no more than 80 bits and the smallest, Single, only 32!), you can only store a limited amount of discrete values, so it is not nearly a continuum. Most real numbers can only (roughly) be approximated by floating point types. Everyone using them should always be aware of this.Some developers, when encountering a problem, say: “I know, I’ll use floating-point numbers !” Now, they have 1.9999999997 problems. — unknown
There are several ways in which real numbers can be represented. In written form, the usual way is to represent them as a string of digits, and the decimal point is represented by a ‘.’, e.g. 12345.678 or 0.0000345. Another way is to use scientific notation, which means that the number is scaled by powers of 10 to, usually, a number between 1 and 10, e.g. 12345.678 is represented as 1.2345678 × 104 or, in short form (the one Delphi uses), as 1.2345678e4.
Internal representation
The way such "real" numbers are represented internally differs a bit from the written notation. The fixed point type Currency is simply stored as a 64 bit integer, but by convention its decimal point is said to be 4 places from the right, i.e. you must divide the integer by 10000 to get the value it is supposed to represent. So the number 3.76 is internally stored as 37600. The type was meant to be used for currencies, but that the type only has 4 decimals means that calculations other than addition or subtraction can cause inaccuracies that are often not tolerable.
The floating point types used in Delphi have an internal representation that is much more like scientific notation. There is an unsigned integer (its size in bit depends on the type) that represents the digits of the number, the mantissa, and a number that represents the scale, in our case in powers of 2 instead of 10, the exponent. There is also a separate sign bit, which is 1 if the number is negative. So in floating point, a number can be represented as:
value = (−1)sign × (mantissa / 2len−1) × 2exp
where sign is the value of the sign bit, mantissa is the mantissa as unsigned integer (more about this later), len is the length of the mantissa in bits, and exp is the exponent.
Mantissa
The mantissa (The IEEE calls it “significand”, but this is a neologism which means something like “which is to be signified”, and in my opinion, that doesn’t make any sense) can be viewed in two ways. Let’s disregard the exponent for the moment, and assume that its value is thus that the number 1.75 is represented by the mantissa. Many texts will tell you that the implicit binary point is viewed to be directly right of the topmost bit of the mantissa, i.e. that the topmost bit represents 20, the one below that 2−1, etc., so a mantissa of binary 1.1100 0000 0000 000 represents 1.0 + 0.5 + 0.25 = 1.75.
Other, but not so many texts, simply treat the mantissa as an unsigned integer, scaled by 2len−1, where len is the size of the mantissa in bits. In other words, a mantissa of 1110 0000 0000 0000 binary or 57344 in decimal is scaled by 215 = 32768 to give you 57344 / 32768 = 1.75 too. As you see, it doesn’t really matter how you approach it, the result is the same.
Exponent
The exponent is the power of 2 by which the mantissa must be multiplied to get the number that is represented. Internally, the exponent is often “biased”, i.e. it is not stored as a signed number, it is stored as unsigned, and the extremes often have special meanings for the number. This means that, to get the actual value of the exponent, you must subtract a constant value from the stored exponent. For instance, the bias for Single is 127. The value of the bias depends on the size of the exponent in bits and is chosen thus, that the smallest normalized value (more about that later) can be reciprocated without overflow.
There are also floating point systems that have a decimal based exponent, i.e. where the value of the exponent represents powers of 10. Examples are the Decimal type used in certain databases and the — slightly incompatible — Decimal type used in Microsoft .NET. The latter uses a 96 bit integer to represent the digits, 1 bit to represent the sign (+ or −) and 5 bits to represent a negative power of 10 (0 up to 28).
The number 123.45678 is represented as 12345678 × 10−5. I have written an almost exact native copy of the Decimal type to be used by Delphi. It is a little faster than the original .NET type, but not nearly as fast as the hardware supported types.
This article mainly discusses the floating point types used in Delphi, to know Single, Double and Extended, which are all floating binary point types. Floating decimal point types like Decimal are not supported by the hardware or by Delphi. So if, in this article, I speak of "floating point" I mean the floating binary point types.
Sign bit
The sign bit is quite simple. If the bit is 1, the number is negative, otherwise it is positive. It is totally independent of the mantissa, so there is no need for a Для просмотра ссылки Войди
Normalization and the hidden bit
I’ll try to explain normalization and denormals with normal scientific notation first.
Take the values 6.123 × 10−22, 612.3 × 10−24 and 61.23 × 10−23 (or 6.123e-22, 612.3e-24 and 61.23e-23 respectively). They all denote the same value, but they have a different representation. To avoid this, let’s make a rule that there can only be one (non-zero) digit to the left of the decimal point. This is called normalization.
Something similar is done with binary floating point too. Since this is binary, there is only one digit left: 1. So there can only be one (non-zero) digit (always 1) to the left of the binary point. Since this is always the same digit, it does not have to be stored, it can be implied. This is the so-called hidden bit. The types Single and Double do not store that bit, but assume it is there in calculations.
How is this done in binary? Let’s take the number 0.375. This can be calculated as 2−2 + 2−3 (0.25 + 0.125), or, in a mantissa, 0.011…bin (disregarding the trailing zeroes), i.e. 0.375 × 20. But this is not how floating point numbers are usually stored. The exponent is adjusted thus, that the mantissa always has its top bit set, except for some special numbers, like 0 or the so called “tiny” (denormalized) values. So the mantissa becomes 1.100…bin and the exponent is decremented by 2.
This number still represents the value 0.375, but now as 1.5 × 2−2. This is how normalization works for binary floating point. It ensures that 1.0 <= mantissa (including hidden bit) < 2.0. Because of the hidden bit, to calculate the value of such a floating point type, you must mentally put the implicit “1.bin” in front of the stored bits of the mantissa.
Note that in e.g. the language C, the value FLT_MIN stands for the smallest (positive) normalized value. You can have values smaller than that, but they will be denormal values, i.e. with a lower precision than 24 bits.
There is some confusion about how to denote the size (or length, as it is often called) of the mantissa of a type with a hidden bit. Some will use the actually stored length in bits, while others also count the hidden bit. For instance, a Single has 23 bits of storage reserved for the mantissa. Some will call the length of the mantissa 23, while others will count the hidden bit too and call it a length of 24.
[/SHOWTOGROUPS]