A New Implementation for a Fast Hash Table
HaniAmmar - 29/Jul/2020
HaniAmmar - 29/Jul/2020
[SHOWTOGROUPS=4,20,22]
A merge of an array and a fast hash table
A data structure that looks like an ordered array and behaves like a hash. Any value can be accessed by its index or by its name. It preserves order of the elements and uses one heap. Therefore, is has an initial. Collisions do not cause new allocations. Instead, every item points to the next one. When expanded, it performs collection and resets its hash base to the new size.
Introduction
Hash tables are data structures that enable locating values using string keys. Some hash tables are fast in insertion, and some in finding values. A few implementations suffer from slow deletion, memory fragmentation, or their performance degrade with more items. Most hash tables do not store items by order, or retrieve a value using an index, and have to consume more memory for fast searching or to keep track of the order if they support that. However, this implementation may offer more speed with less trading.
Implementation
For a data structure to retrieve values using numbers, it needs to be a linear array, and when its memory block reaches its limit, it expands to a new heap and moves all of its items from the old memory to the new one. Therefore, it has to be a one-dimensional array. It is not an array or a hash table, but both:
template <typename Value_>
struct HArray {
size_t size_{0};
size_t capacity_{0};
Value_ *storage_{nullptr};
};
The variable size_ holds the number of items, capacity_ is for the size of the heap/memory block, and storage_ points to the location of the first value. Still, items have to store more than just values; they need the variable key_ and its hash for HArray to function as a hash table.
Hide Copy Code
template <typename Key_, typename Value_>
struct HAItem {
size_t hash_;
Key_ key_;
Value_ value_;
};
template <typename Key_, typename Value_>
struct HArray {
size_t size_{0};
size_t capacity_{0};
HAItem<Key_, Value_> *storage_{nullptr};
};
A linear array insertion looks like the following:
Hide Copy Code
private:
void insert_(Key_ key, Value_ value, size_t hash) {
if (size_ == capacity_) {
// expand
}
HAItem<Key_, Value_> &item = storage_[size_];
item.hash_ = hash;
item.key_ = key;
item.value_ = value;
++size_;
}
But, for the hash table to work, it needs a searching technique and deals with collisions. One way to solve that is to add a linked list by adding an extra variable next_ to the structure, to point to the item that comes next. Therefore, the new structure looks like:
Hide Copy Code
template <typename Key_, typename Value_>
struct HAItem {
size_t hash_;
HAItem *next_;
Key_ key_;
Value_ value_;
};
The searching technique compares a given key to a stored one. It locates it by dividing its hash value over (capacity – 1) and the remainder – of that division point to an index, a location in the allocated heap. If the compare function sought that the two keys are different, then it checks the pointer next_ to see if its item holds the same key or not, and keep on looking until it finds it or hit a null pointer. However, an infinite loop could occur.
Assume capacity_ is 21, and there are two items to be inserted: item1 has a hash value equal to 41, and item2 has its hash set to 60. The location of item1 is 41 % (21 - 1) = 41 % 20 = 1. The algorithm will lookup index 1 and set the last/null next_ pointer to point to item1. For item2, 60 % 20 = 0, thus, storage_[0].next_ is set to point to item2; assuming next_ is null. Now, if a new item comes in with a hash value of 20, 40, 21, 41 … it will point to either item1 or item2, and when it does, it will see item1 pointing to item2 and item2.next_ pointing back to item1, and when it tries to find the end of the linked list, it will end up in an infinite loop.
That is fixable by storing the start address, and checking every next_ variable, then break the loop if they match, then insert the new item between the last next_ and the one after it (it could be null). However, there is a faster way, and that way is by adding another pointer named anchor_. Therefore, the final structure of HAItem looks like:
Hide Copy Code
template <typename Key_, typename Value_>
struct HAItem {
HAItem *anchor_{nullptr};
size_t hash_{0};
HAItem *next_{nullptr};
Key_ key_{};
Value_ value_{};
};
Now next_ is for collision only, and anchor_ points to the location of the item. With that, next_ will point to forward elements (1, 2, 3, 4, 5), and CPU prefetching may bring the next item, while the search function is comparing the given key with the current item’s key_. However, anchor_ could point to anyone at that heap, and if it is null, then the item does not exist.
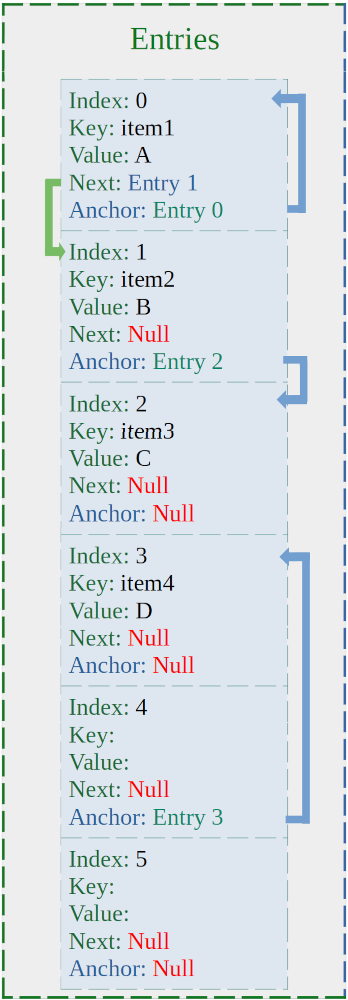
To understand the concept, assume that we have an array that has the capacity of 6 elements, and we need to insert the following items:
The base for the hash table is (capacity – 1), which is 5. item1 is inserted in location 0 - because 10 % 5 is 0, hence, storage_[0].anchor_ = the pointer of index 0. item2 is inserted at index 1, but its hash result points to 0 (15 % 5 = 0), the search function will lookup index 0 and finds item1, then it checks its next_ pointer to find the final pointer that has a null value and set it to point to item2. item3 is placed in index 3, and its hash points to index 1. Even though there is an item in index 1, its anchor_ is null, and the function will set storage_[1].anchor_ to point to item3. item4 will get the index 3, and its hash result points to index 4, therefore, storage_[0].anchor_ = &item3. And the data looks like:
[/SHOWTOGROUPS]
A merge of an array and a fast hash table
A data structure that looks like an ordered array and behaves like a hash. Any value can be accessed by its index or by its name. It preserves order of the elements and uses one heap. Therefore, is has an initial. Collisions do not cause new allocations. Instead, every item points to the next one. When expanded, it performs collection and resets its hash base to the new size.
Introduction
Hash tables are data structures that enable locating values using string keys. Some hash tables are fast in insertion, and some in finding values. A few implementations suffer from slow deletion, memory fragmentation, or their performance degrade with more items. Most hash tables do not store items by order, or retrieve a value using an index, and have to consume more memory for fast searching or to keep track of the order if they support that. However, this implementation may offer more speed with less trading.
Implementation
For a data structure to retrieve values using numbers, it needs to be a linear array, and when its memory block reaches its limit, it expands to a new heap and moves all of its items from the old memory to the new one. Therefore, it has to be a one-dimensional array. It is not an array or a hash table, but both:
template <typename Value_>
struct HArray {
size_t size_{0};
size_t capacity_{0};
Value_ *storage_{nullptr};
};
The variable size_ holds the number of items, capacity_ is for the size of the heap/memory block, and storage_ points to the location of the first value. Still, items have to store more than just values; they need the variable key_ and its hash for HArray to function as a hash table.
Hide Copy Code
template <typename Key_, typename Value_>
struct HAItem {
size_t hash_;
Key_ key_;
Value_ value_;
};
template <typename Key_, typename Value_>
struct HArray {
size_t size_{0};
size_t capacity_{0};
HAItem<Key_, Value_> *storage_{nullptr};
};
A linear array insertion looks like the following:
Hide Copy Code
private:
void insert_(Key_ key, Value_ value, size_t hash) {
if (size_ == capacity_) {
// expand
}
HAItem<Key_, Value_> &item = storage_[size_];
item.hash_ = hash;
item.key_ = key;
item.value_ = value;
++size_;
}
But, for the hash table to work, it needs a searching technique and deals with collisions. One way to solve that is to add a linked list by adding an extra variable next_ to the structure, to point to the item that comes next. Therefore, the new structure looks like:
Hide Copy Code
template <typename Key_, typename Value_>
struct HAItem {
size_t hash_;
HAItem *next_;
Key_ key_;
Value_ value_;
};
The searching technique compares a given key to a stored one. It locates it by dividing its hash value over (capacity – 1) and the remainder – of that division point to an index, a location in the allocated heap. If the compare function sought that the two keys are different, then it checks the pointer next_ to see if its item holds the same key or not, and keep on looking until it finds it or hit a null pointer. However, an infinite loop could occur.
Assume capacity_ is 21, and there are two items to be inserted: item1 has a hash value equal to 41, and item2 has its hash set to 60. The location of item1 is 41 % (21 - 1) = 41 % 20 = 1. The algorithm will lookup index 1 and set the last/null next_ pointer to point to item1. For item2, 60 % 20 = 0, thus, storage_[0].next_ is set to point to item2; assuming next_ is null. Now, if a new item comes in with a hash value of 20, 40, 21, 41 … it will point to either item1 or item2, and when it does, it will see item1 pointing to item2 and item2.next_ pointing back to item1, and when it tries to find the end of the linked list, it will end up in an infinite loop.
That is fixable by storing the start address, and checking every next_ variable, then break the loop if they match, then insert the new item between the last next_ and the one after it (it could be null). However, there is a faster way, and that way is by adding another pointer named anchor_. Therefore, the final structure of HAItem looks like:
Hide Copy Code
template <typename Key_, typename Value_>
struct HAItem {
HAItem *anchor_{nullptr};
size_t hash_{0};
HAItem *next_{nullptr};
Key_ key_{};
Value_ value_{};
};
Now next_ is for collision only, and anchor_ points to the location of the item. With that, next_ will point to forward elements (1, 2, 3, 4, 5), and CPU prefetching may bring the next item, while the search function is comparing the given key with the current item’s key_. However, anchor_ could point to anyone at that heap, and if it is null, then the item does not exist.
To understand the concept, assume that we have an array that has the capacity of 6 elements, and we need to insert the following items:
key | Value | Hash |
|---|---|---|
item1 | A | 10 |
item2 | B | 15 |
item3 | C | 21 |
item4 | D | 24 |
[/SHOWTOGROUPS]